Kuinka lukea binääriä

Jos olet kiinnostunut oppimaan lukemaan binäärilukuja, on tärkeää ymmärtää, miten binääriluvut toimivat. Binaari tunnetaan «perus 2» -numerojärjestelmänä, mikä tarkoittaa, että jokaiselle numerolle on kaksi mahdollista numeroa; yksi tai nolla. Suuremmat luvut kirjoitetaan lisäämällä binäärilukuun ylimääräisiä ykkösiä tai nollia.

Binäärilukujen ymmärtäminen

Binaarilukujen osaaminen ei ole välttämätöntä tietokoneiden käyttämiselle. Mutta on hyvä ymmärtää käsite, jotta saat paremman käsityksen siitä, kuinka tietokoneet tallentavat numeroita muistiin. Sen avulla voit myös ymmärtää termejä, kuten 16-bittinen, 32-bittinen, 64-bittinen ja muistimittauksia, kuten tavuja (8 bittiä).

Kuinka lukea binaarikoodia

Binäärikoodin «lukeminen» tarkoittaa tyypillisesti binääriluvun muuntamista 10 (desimaali) luvuksi, jonka ihmiset tietävät. Tämä muunnos on tarpeeksi helppo tehdä päässäsi, kun ymmärrät kuinka binäärikieli toimii.b Jokaisella binääriluvun numeropaikalla on tietty arvo, jos numero ei ole nolla. Kun olet määrittänyt kaikki nämä arvot, lisää ne yhteen saadaksesi binääriluvun 10 (desimaali). Jos haluat nähdä, kuinka tämä toimii, ota binääriluku 110010.

1. Paras tapa lukea binääriluku on aloittaa oikealla olevasta numerosta ja siirtyä vasemmalle. Ensimmäisen paikan teho on nolla, mikä tarkoittaa, että jos se ei ole nolla, kyseisen numeron arvo on kahdesta nollaan, tai yksi. Tässä tapauksessa, koska numero on nolla, tämän paikan arvo olisi nolla.

2. Siirry sitten seuraavaan numeroon. Jos se on yksi, laske kaksi yhden potenssilla. Huomaa myös tämä arvo. Tässä esimerkissä arvo on kaksi potenssilla yksi, joka on kaksi.

   

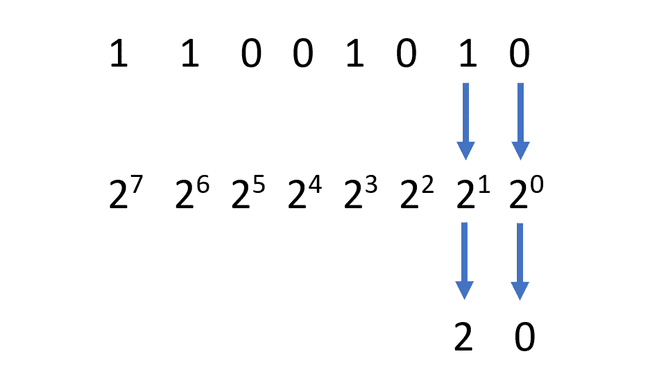
3. Toista tätä prosessia, kunnes pääset vasemmanpuoleisimpaan numeroon.

   

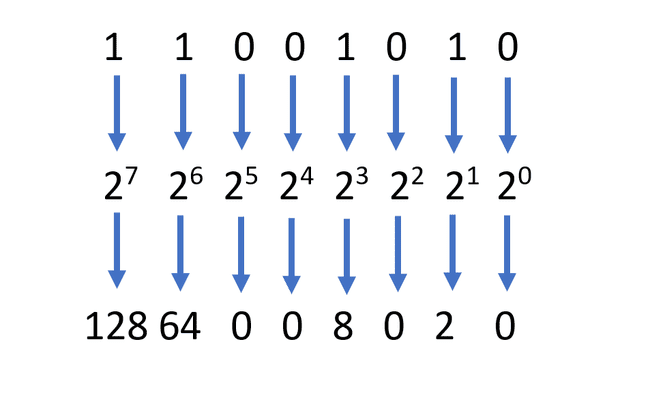
4. Lopuksi sinun tarvitsee vain lisätä kaikki nämä luvut yhteen saadaksesi binääriluvun kokonaisdesimaaliarvon: 128 + 64 + 0 + 0 + 8 + 0 + 2 + 0 = 202

   Toinen tapa nähdä tämä koko prosessi yhtälömuodossa on seuraava: 1 x 2⁷ + 1 x 2⁶ + 0 x 2⁵ + 0 x 2⁴ + 1 x 2³ + 0 x 2² + 1 x 2¹ + 0 x 2⁰ = 202

Allekirjoitetut binääriluvut

Yllä oleva menetelmä toimii yksinkertaisille, etumerkittömille binääriluvuille. Tietokoneet tarvitsevat kuitenkin tavan esittää negatiivisia lukuja myös binäärimuodossa. Tästä syystä tietokoneet käyttävät etumerkillisiä binäärilukuja. Tämän tyyppisessä järjestelmässä vasemmanpuoleisin numero tunnetaan etumerkkibittinä, kun taas loput numerot tunnetaan kokobitteinä. Etumerkillisen binääriluvun lukeminen on melkein sama kuin etumerkittömän, pienellä erolla.

1. Suorita sama toimenpide kuin edellä on kuvattu etumerkittömälle binääriluvulle, mutta lopeta heti, kun saavutat vasemmanpuoleisimman bitin.

   

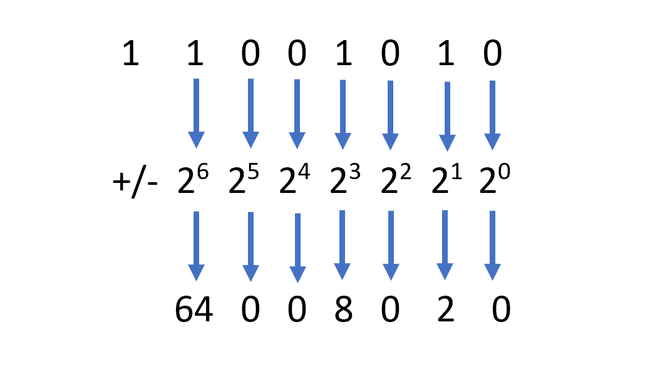
2. Voit määrittää merkin tarkastelemalla vasemmanpuoleista bittiä. Jos se on yksi, luku on negatiivinen. Jos se on nolla, luku on positiivinen.

   

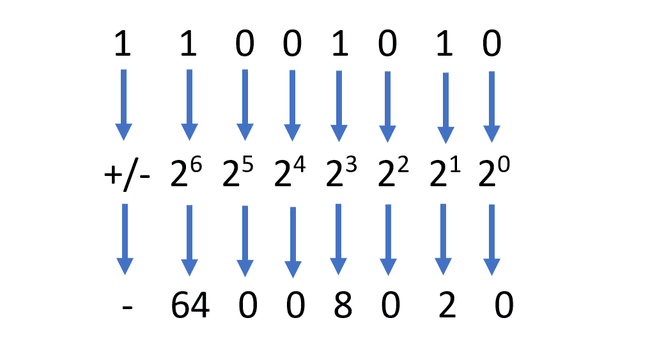
3. Suorita nyt sama laskutoimitus kuin aiemmin, mutta käytä oikeaa etumerkkiä numeroon vasemmanpuoleisen bitin osoittamalla tavalla: 64 + 0 + 0 + 8 + 0 + 2 + 0 = -74

4. Signed binary -menetelmän avulla tietokoneet voivat näyttää numeroita, jotka ovat positiivisia tai negatiivisia. Se kuitenkin kuluttaa ensimmäisen bitin, mikä tarkoittaa, että suuremmat luvut vaativat hieman enemmän muistia kuin etumerkitmättömät binääriluvut.