Tee T-testi Excelissä

T-testi on tapa määrittää, onko aineistojen välillä tilastollisesti merkittäviä eroja Studentin t-jakauman avulla. Excelin T-testi on kahden otoksen t-testi, joka vertaa kahden näytteen keskiarvoja. Tässä artikkelissa kerrotaan, mitä tilastollinen merkitsevyys tarkoittaa ja kuinka voit tehdä T-testin Excelissä. Tämän artikkelin ohjeet koskevat Excel 2019, 2016, 2013, 2010, 2007; Excel Microsoft 365:lle ja Excel Onlinelle.

Mikä on tilastollinen merkitsevyys?

Oletetaan, että haluat tietää, kumpi kahdesta nopasta antaa paremman pistemäärän. Heität ensimmäisen noppaa ja saat 2; Heität toista noppaa ja saat 6. Tarkoittaako tämä sitä, että toinen noppa antaa yleensä korkeammat pisteet? Jos vastasit «Ei tietenkään», sinulla on jo jonkinlainen käsitys tilastollisesta merkityksestä. Ymmärrät, että ero johtui pistemäärän satunnaisesta muutoksesta joka kerta kun noppaa heitetään. Koska näyte oli hyvin pieni (vain yksi rulla), se ei osoittanut mitään merkittävää. Kuvittele nyt, että heittäisit jokaista noppaa 6 kertaa:

• Ensimmäinen meisti pyörii 3, 6, 6, 4, 3, 3; Keskiarvo = 4,17
• Toinen meisti rullaa 5, 6, 2, 5, 2, 4; Keskiarvo = 4,00

Todistaako tämä, että ensimmäinen kuoppa antaa korkeammat pisteet kuin toinen? Luultavasti ei. Pieni otos, jossa on suhteellisen pieni ero keskiarvojen välillä, tekee todennäköiseksi, että ero johtuu edelleen satunnaisista vaihteluista. Kun lisäämme noppien määrää, on vaikea antaa tervettä järkeä olevaa vastausta kysymykseen: Onko tulosero satunnaisvaihtelun tulosta vai saako toinen todennäköisemmin korkeamman tuloksen kuin toinen? Merkittävyys on todennäköisyys, että havaittu ero näytteiden välillä johtuu satunnaisista vaihteluista. Merkitystä kutsutaan usein alfa-tasoksi tai yksinkertaisesti ‘α:ksi. Luottamustaso tai yksinkertaisesti ‘c’ on todennäköisyys sille, että näytteiden välinen ero ei johdu satunnaisvaihtelusta; toisin sanoen, että taustalla olevien populaatioiden välillä on ero. Siksi: C = 1 – α

Voimme asettaa «α» mille tahansa tasolle, jonka haluamme varmistaa, että meillä on todistettu merkitys. Hyvin usein käytetään arvoa α=5 % (95 %:n luottamus), mutta jos todella haluamme olla varmoja siitä, että erot eivät johdu satunnaisvaihtelusta, voidaan käyttää korkeampaa luottamustasoa, α=1 % tai jopa α=0,1. %. Eri tilanteiden merkitsevyyden laskemiseen käytetään erilaisia ​​tilastollisia testejä. T-testejä käytetään määrittämään, ovatko kahden populaation keskiarvot erilaiset, ja F-testejä käytetään määrittämään, ovatko varianssit erilaisia.

Miksi tilastollista merkitsevyyttä testataan?

Kun vertaamme eri asioita, meidän on käytettävä merkitsevyystestejä määrittääksemme, onko toinen parempi kuin toinen. Tämä koskee monia kenttiä, esimerkiksi:

• Liiketoiminnassa ihmisten on verrattava erilaisia ​​tuotteita ja markkinointimenetelmiä.
• Urheilussa ihmisten on verrattava erilaisia ​​laitteita, tekniikoita ja kilpailijoita.
• Suunnittelussa ihmisten on verrattava erilaisia ​​malleja ja parametriasetuksia.

Jos haluat testata, menestyykö jokin jollakin alueella jotain muuta, sinun on testattava tilastollinen merkitsevyys.

Mikä on opiskelijan T-jakauma?

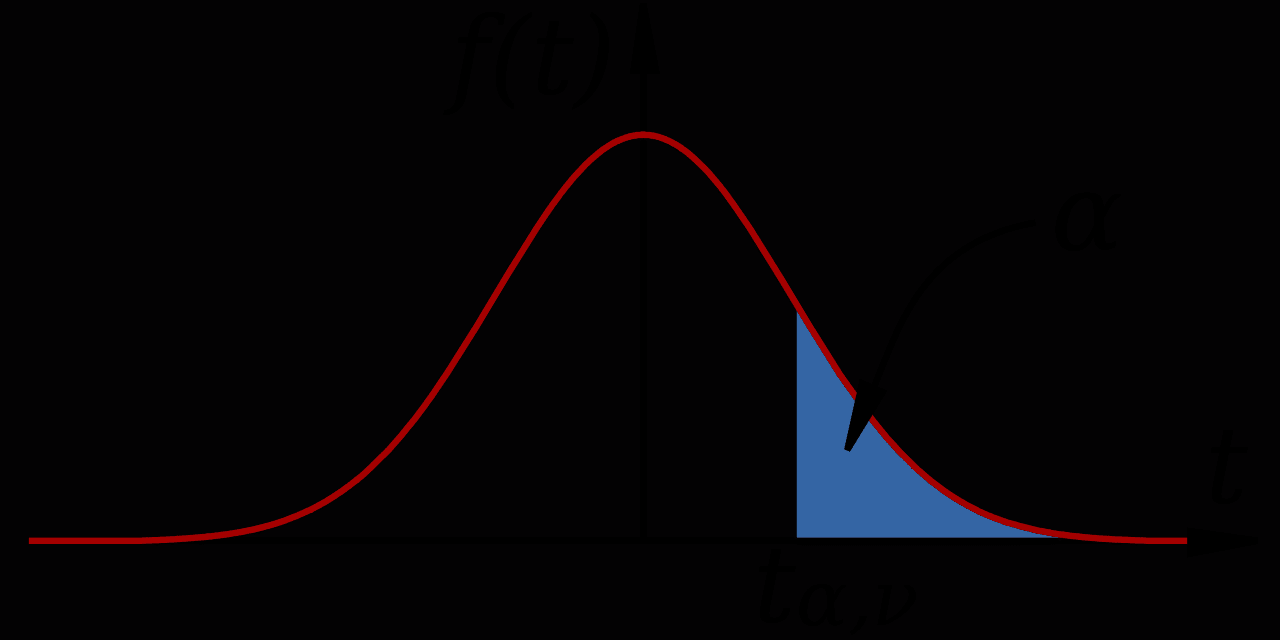
Studentin t-jakauma on samanlainen kuin normaali (tai Gaussin) jakauma. Nämä ovat molemmat kellon muotoisia jakaumia, joissa useimmat tulokset ovat lähellä keskiarvoa, mutta jotkin harvinaiset tapahtumat ovat melko kaukana keskiarvosta molempiin suuntiin, joita kutsutaan jakauman hännäksi. Studentin t-jakauman tarkka muoto riippuu otoksen koosta. Yli 30 näytteille se on hyvin samanlainen kuin normaalijakauma. Kun otoskoko pienenee, hännät kasvavat, mikä edustaa suurempaa epävarmuutta, joka syntyy pieneen otokseen perustuvien päätelmien tekemisestä.

T-testin tekeminen Excelissä

Ennen kuin voit käyttää T-testiä määrittääksesi, onko kahden näytteen keskiarvojen välillä tilastollisesti merkitsevä ero, sinun on ensin suoritettava F-testi. Tämä johtuu siitä, että T-testille suoritetaan erilaisia ​​laskelmia sen mukaan, onko varianssien välillä merkittävää eroa. tarvitset Analyysityökalupaketin lisäosa pystyy suorittamaan tämän analyysin.

Tarkistetaan ja ladataan Analysis Toolpak -apuohjelmaa

Tarkista ja aktivoi analyysityökalupaketti seuraavasti:

1. Valitse TIEDOSTO välilehti > valitse Vaihtoehdot†

2. Valitse Asetukset-valintaikkunassa Plugins vasemmalla olevien välilehtien kautta.

3. Valitse ikkunan alareunasta Hallinnoi avattavasta valikosta ja valitse sitten Excelin lisäosat† Valitse Mennä†

   

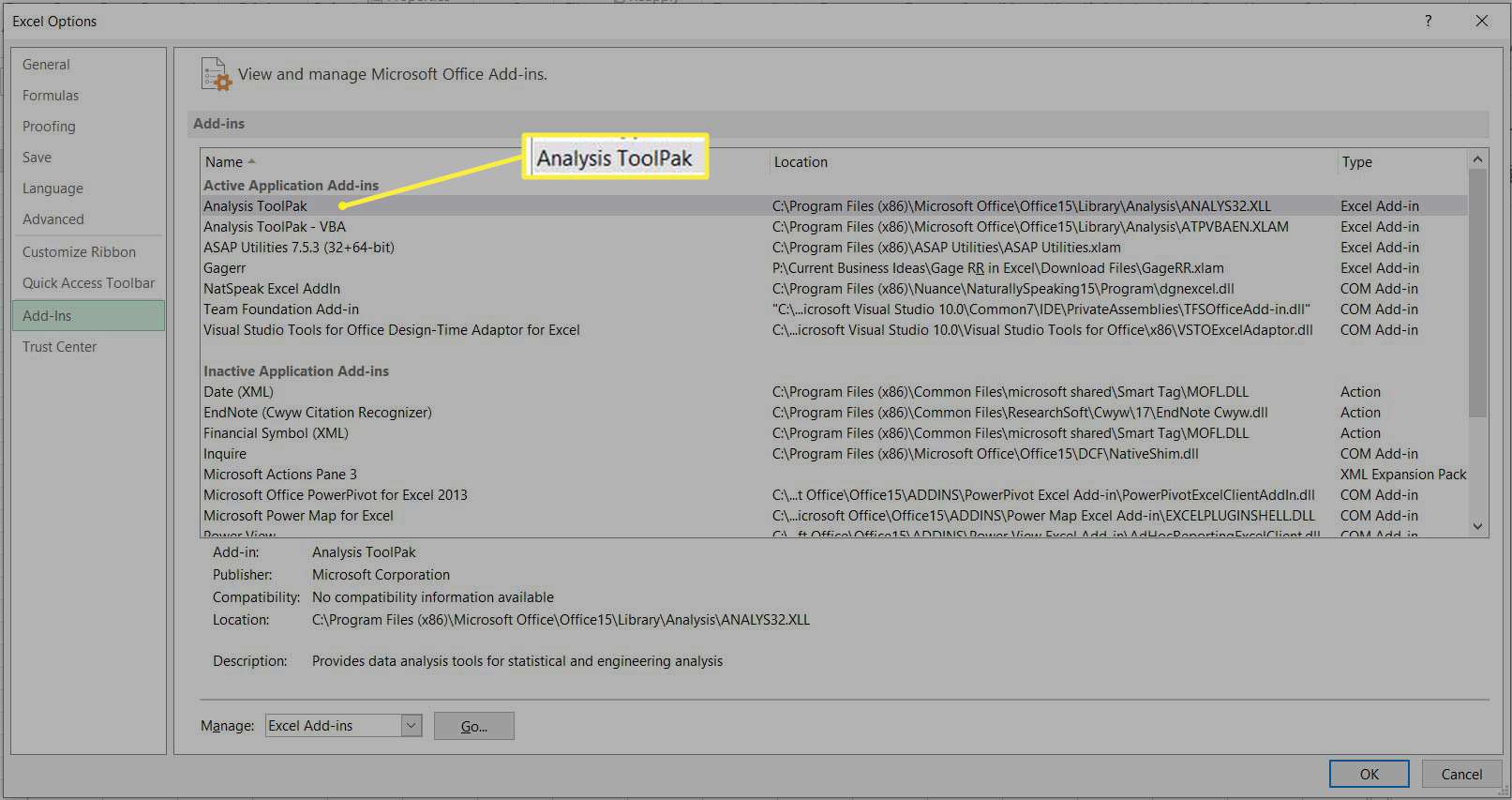
4. Varmista, että valintaruutu on vieressä Analyysityökalupaketti on valittuna ja valitse sitten Okei†

5. Analyysityökalupaketti on nyt aktiivinen ja olet valmis käyttämään F-testejä ja T-testejä.

F-testin ja T-testin suorittaminen Excelissä

1. Syötä kaksi tietojoukkoa laskentataulukkoon. Tässä tapauksessa harkitsemme kahden tuotteen myyntiä viikon aikana. Jokaiselle tuotteelle lasketaan myös keskimääräinen päivittäinen myyntiarvo keskihajonnan kanssa.

2. Valitse Faktat välilehti > Tietojen analysointi

3. Valitse F-Test Two-Sample varianssien varalta luettelosta ja valitse sitten Okei†

   

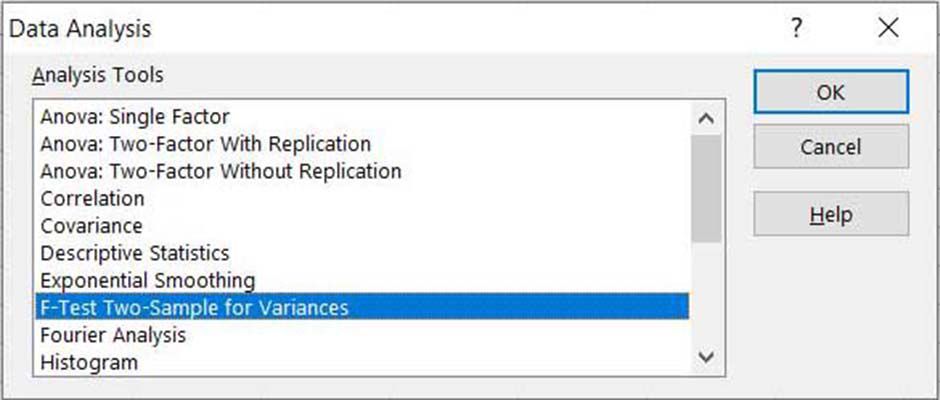
   F-testi on erittäin herkkä epänormaalisuudelle. Siksi voi olla turvallisempaa käyttää Welch-testiä, mutta Excelissä se on vaikeampaa.

4. Valitse muuttujan 1 alue ja muuttujan 2 alue; aseta alfa (0,05 tarkoittaa 95 %:n luottamusta); valitse solu tulosteen vasempaan yläkulmaan, sillä se täyttää 3 saraketta ja 10 riviä. Valitse Okei†

   

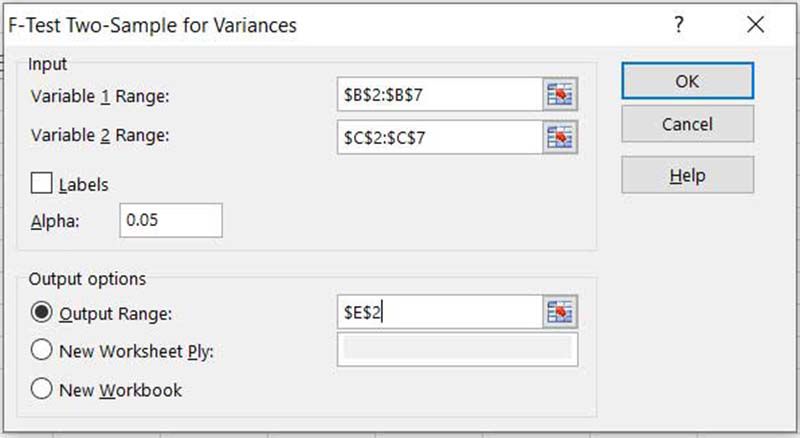
   Muuttujan 1 vaihteluvälille tulee valita otos, jolla on suurin keskihajonna (tai varianssi).

5. Tarkista F-testin tulokset selvittääksesi, onko varianssien välillä merkittävää eroa. Tulokset antavat kolme tärkeää arvoa:

   • f: varianssien välinen suhde.
   • P(F<=f) yksipuolinen: Todennäköisyys, että muuttujalla 1 ei todellakaan ole suurempaa varianssia kuin muuttujalla 2. Jos se on suurempi kuin alfa, joka on yleensä 0,05, niin varianssien välillä ei ole merkittävää eroa.
   • F Yksipuolista kritiikkiä: F:n arvo, joka tarvittaisiin saadakseen P(F<=f)=α. Jos tämä arvo on suurempi kuin F, se osoittaa myös, että varianssien välillä ei ole merkittävää eroa.

   P(F<=f) voidaan myös laskea käyttämällä FDIST-funktiota, jossa F ja kunkin näytteen vapausasteet syötteenä. Vapausasteet ovat yksinkertaisesti havaintojen lukumäärä näytteessä miinus yksi.

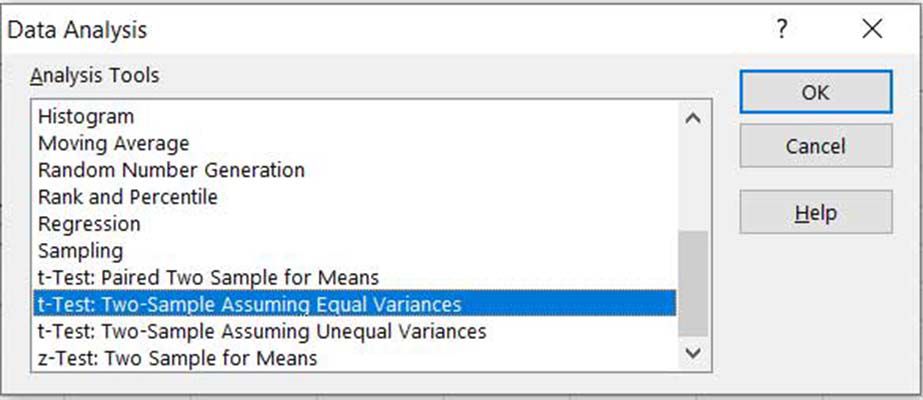
6. Nyt kun tiedät, onko varianssien välillä eroa, voit valita oikean T-testin. Valitse Faktat välilehti > Tietojen analysointija valitse sitten jompikumpi t-testi: kaksi näytettä olettaen yhtä suuret varianssit tai t-testi: kaksi näytettä, joissa oletetaan epäyhtenäiset varianssit†

   

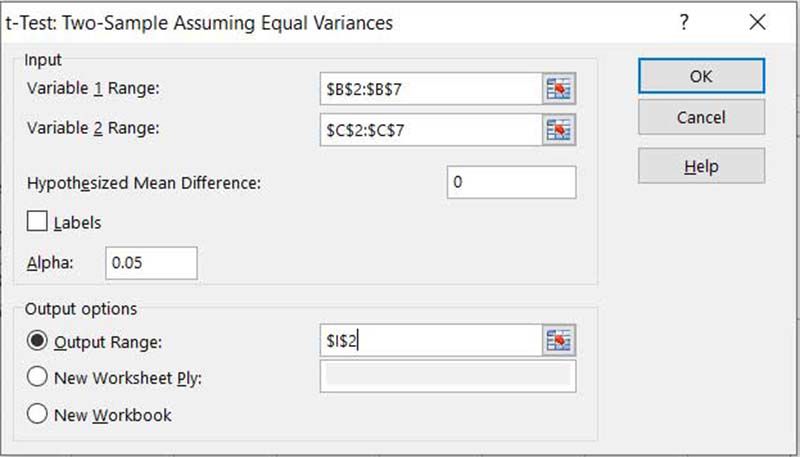
7. Riippumatta siitä, minkä vaihtoehdon valitsit edellisessä vaiheessa, sinulle näytetään sama valintaikkuna, jossa voit syöttää analyysin tiedot. Aloita valitsemalla alueet, joissa on näytteitä Muuttujan 1 alue ja Muuttujan 2 alue†

   

8. Olettaen, että haluat testata, ettei välineiden välillä ole eroa, aseta Hypoteettinen keskimääräinen ero nollaan.

9. Aseta merkitsevyystasoksi Alpha (0,05 antaa 95 %:n varmuuden) ja valitse solu tulosteen vasempaan yläkulmaan, koska se täyttää 3 saraketta ja 14 riviä. Valitse Okei†

10. Tarkista tulokset ja päätä, onko välineiden välillä merkittävää eroa. Kuten F-testissä, jos p-arvo, tässä tapauksessa P(T<=t), on suurempi kuin alfa, ei ole merkittävää eroa. Tässä tapauksessa kuitenkin annetaan kaksi p-arvoa, yksi yksisuuntaiselle testille ja toinen kaksisuuntaiselle testille. Käytä tässä tapauksessa kaksisuuntaista arvoa, koska mikä tahansa muuttuja, jolla on suurempi keskiarvo, olisi merkittävä ero.