Mikä on Excel Solver?

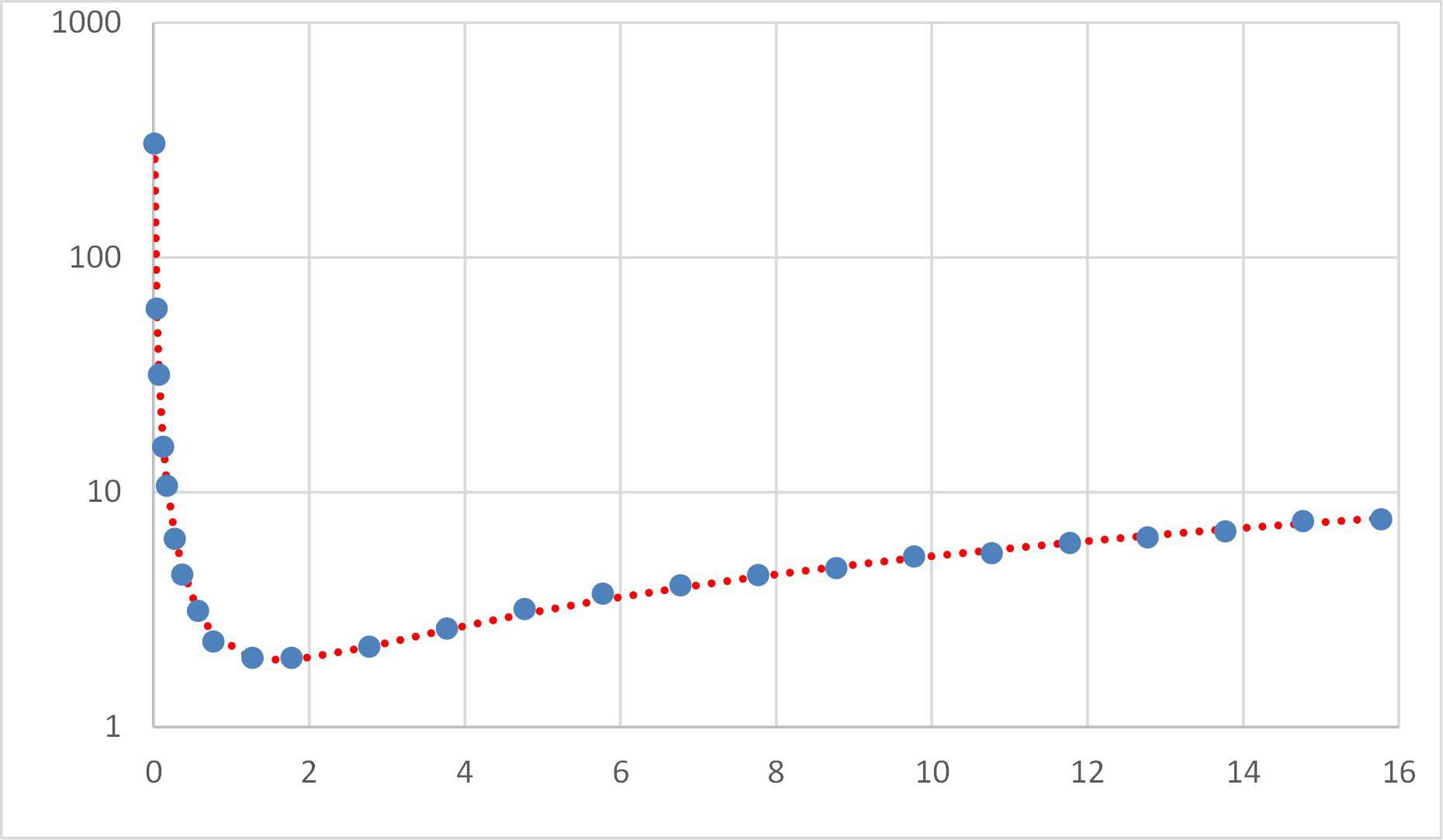
Excel Solver -apuohjelma suorittaa matemaattisen optimoinnin. Tätä käytetään yleensä sovittamaan monimutkaisia ​​malleja dataan tai etsimään iteratiivisia ratkaisuja ongelmiin. Haluat esimerkiksi sovittaa käyrän joidenkin datapisteiden läpi yhtälön avulla. Ratkaisija löytää yhtälöstä vakiot, jotka parhaiten sopivat dataan. Toinen sovellus on, jossa mallia on vaikea järjestää uudelleen niin, että vaadittava tulos tulee yhtälön aiheeksi.

Missä on Excelin Ratkaisija?

Solver-apuohjelma sisältyy Exceliin, mutta se ei aina lataudu osana oletusasennusta. Voit tarkistaa, onko se ladattu, valitsemalla TIEDOT -välilehti ja etsi ratkaisija -kuvaketta Analyysi -osio.

Jos et löydä Ratkaisijaa TIEDOT-välilehdeltä, sinun on ladattava apuohjelma:

1. Valitse TIEDOSTO -välilehti ja valitse sitten Vaihtoehdot†

   

2. Vuonna Vaihtoehdot valitse valintaikkuna Plugins vasemmalla olevien välilehtien kautta.

   

3. Valitse ikkunan alareunasta Excelin lisäosat -lta Hallita avattavasta luettelosta ja valitse Mennä…

   

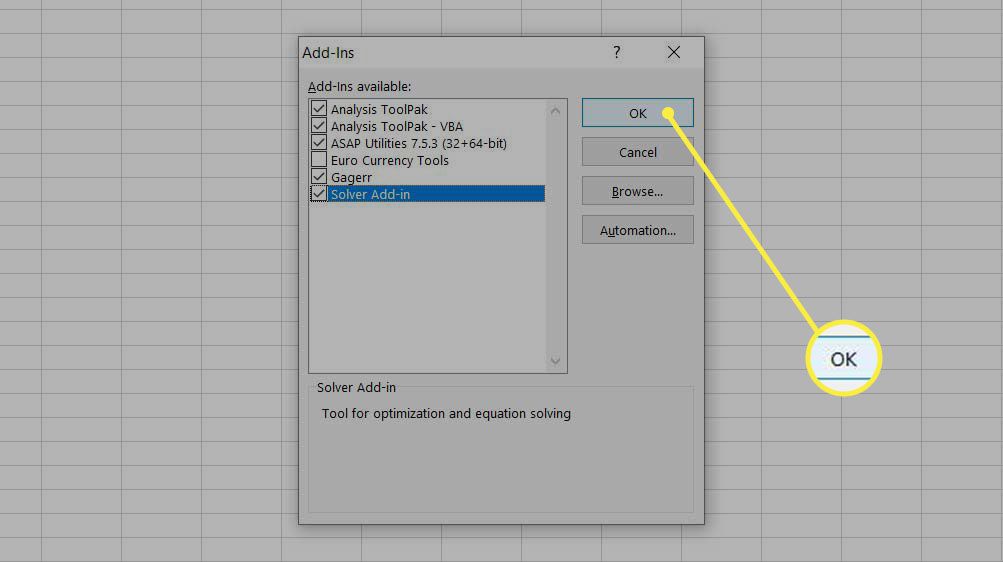
4. Valitse vieressä oleva valintaruutu. klo Ratkaisija-laajennus ja valitse Okei†

   

5. The ratkaisija -komennon pitäisi nyt näkyä TIEDOT -välilehti. Olet valmis käyttämään Solveria.

   

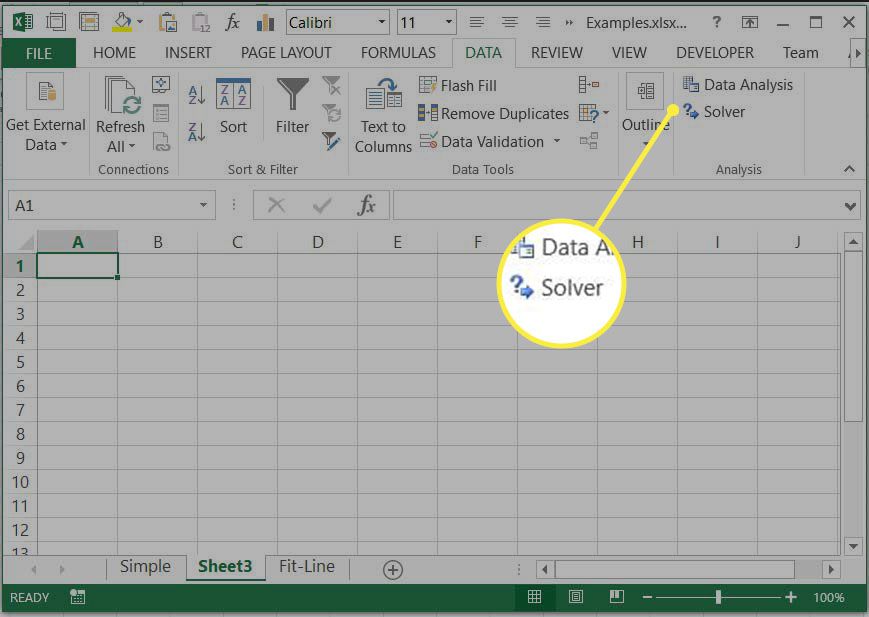
Ratkaisijan käyttäminen Excelissä

Aloitetaan yksinkertaisella esimerkillä ymmärtääksesi, mitä Ratkaisija tekee. Oletetaan, että haluamme tietää, mikä säde antaa ympyrän, jonka pinta-ala on 50 neliöyksikköä. Tiedämme ympyrän alueen yhtälön (A = pi r²† Voimme tietysti järjestää tämän yhtälön uudelleen antamaan tietylle alueelle tarvittavan säteen, mutta oletetaanpa esimerkkinä, että emme tiedä miten se tehdään. Luo laskentataulukko säteellä sisään B1 ja laske ala B2 yhtälön avulla =pi()*B1^2†

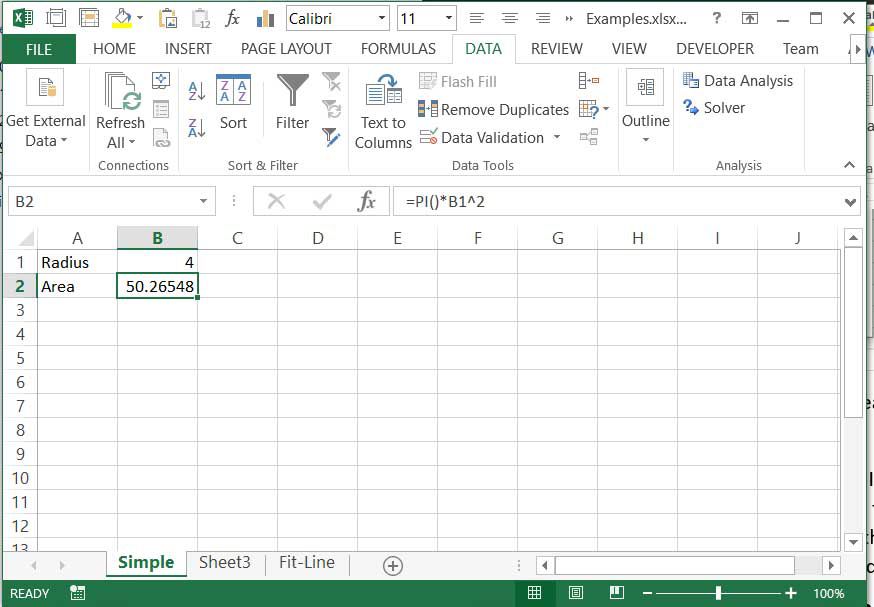
Voimme säätää arvoa manuaalisesti B1 siihen asti kun B2 näyttää arvon, joka on tarpeeksi lähellä 50:tä. Riippuen siitä, kuinka tarkkoja meidän on oltava, tämä voi olla käytännöllinen lähestymistapa. Jos meidän on kuitenkin oltava erittäin tarkkoja, tarvittavien säätöjen tekeminen kestää kauan. Itse asiassa tämä on pohjimmiltaan sitä, mitä Solver tekee. Se säätää tiettyjen solujen arvoja ja tarkistaa arvon kohdesolussa:

1. Valitse TIEDOT välilehti ja ratkaisijaympäri . lastata Ratkaisijan parametrit: valintaikkuna

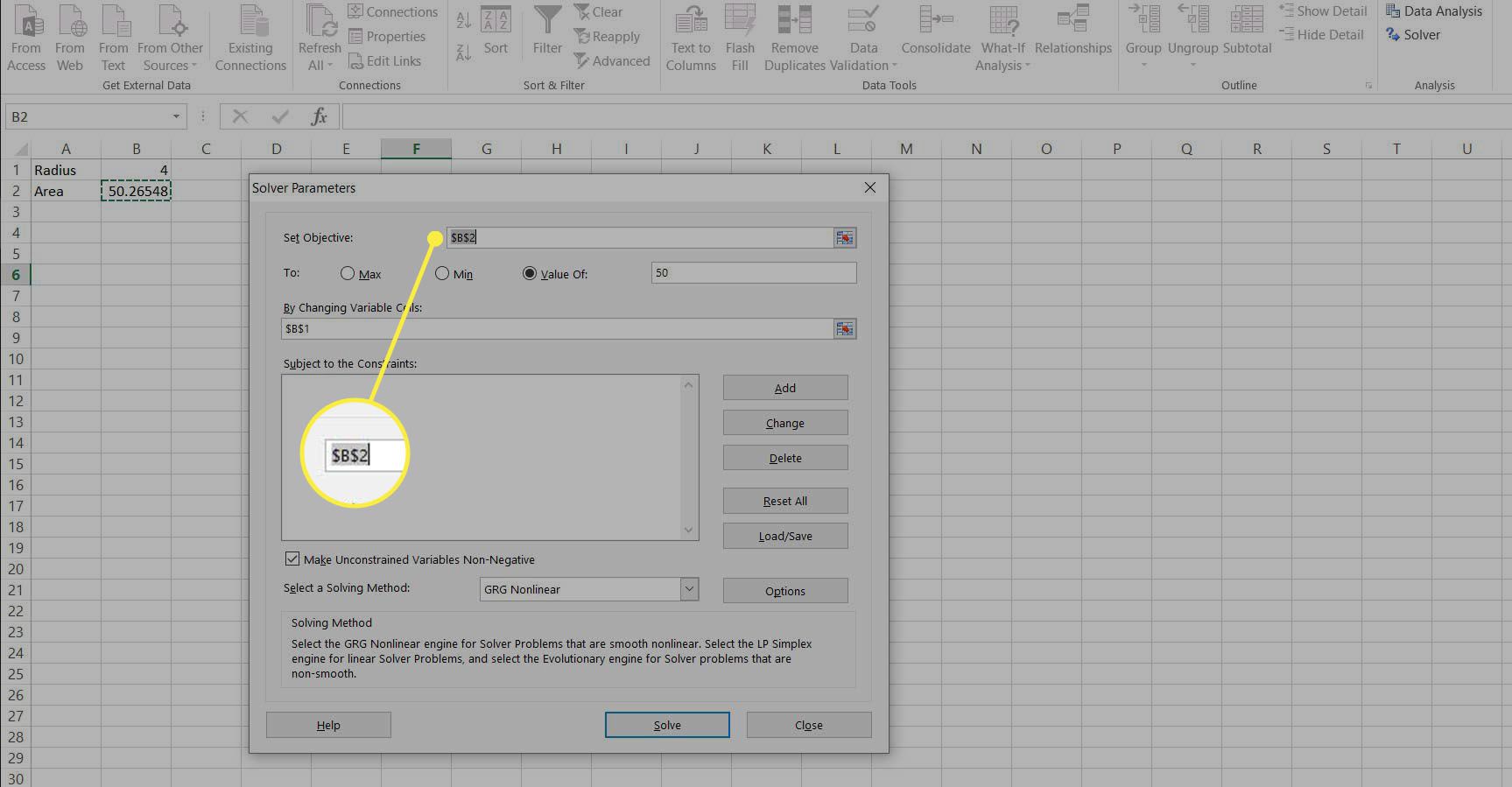
2. asettaa tavoite solu on alue, B2† Tämä on arvo, joka tarkistetaan säätämällä muita soluja, kunnes se saavuttaa oikean arvon.

   

3. Valitse painike Jonkin arvo: ja aseta arvoksi 50. Tämä on arvo, joka B2:n tulisi saavuttaa.

   

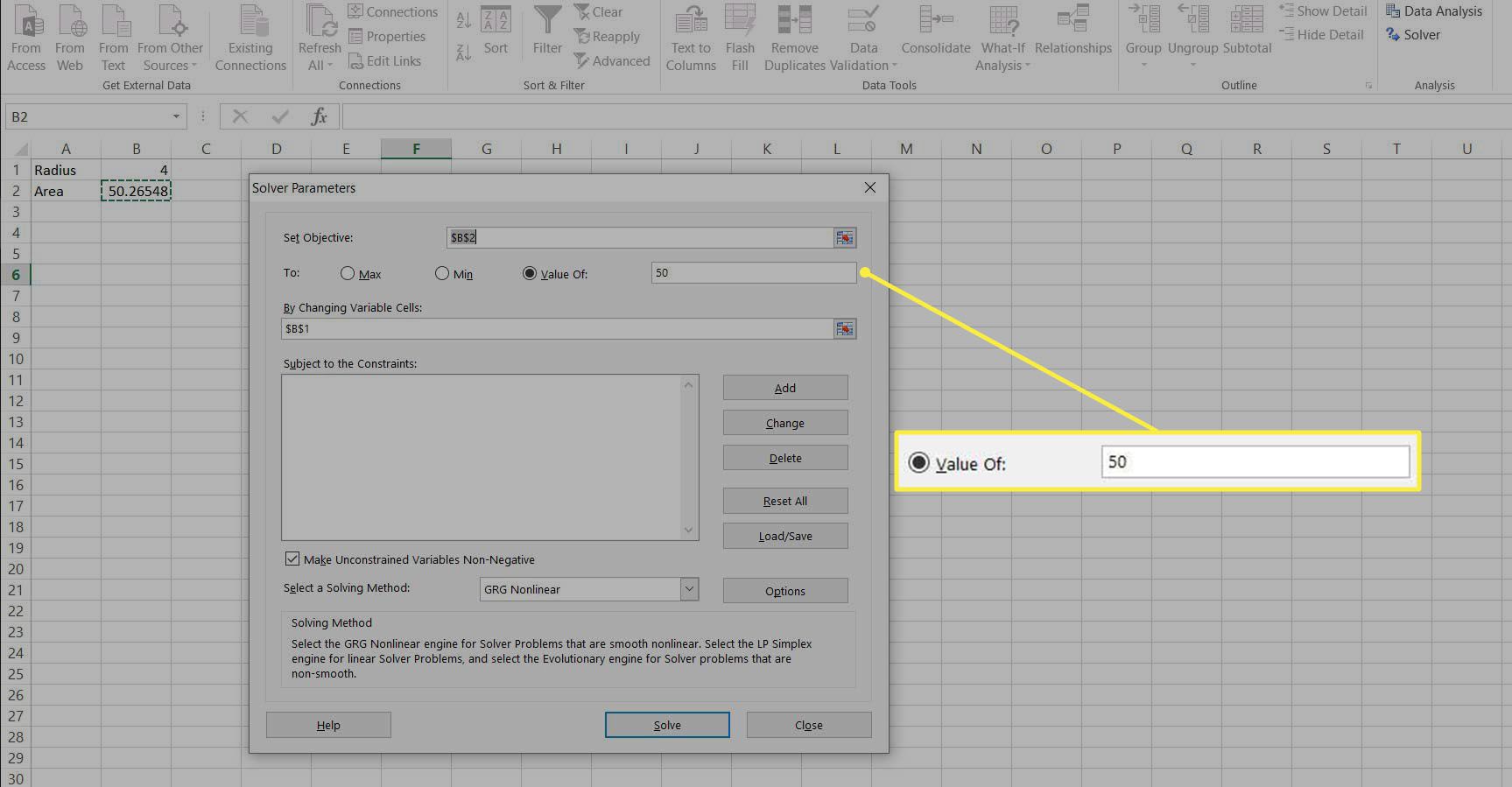
4. Otsikolla varustetussa laatikossa Muuttamalla muuttuvia soluja: syötä soluun säde, B1†

   

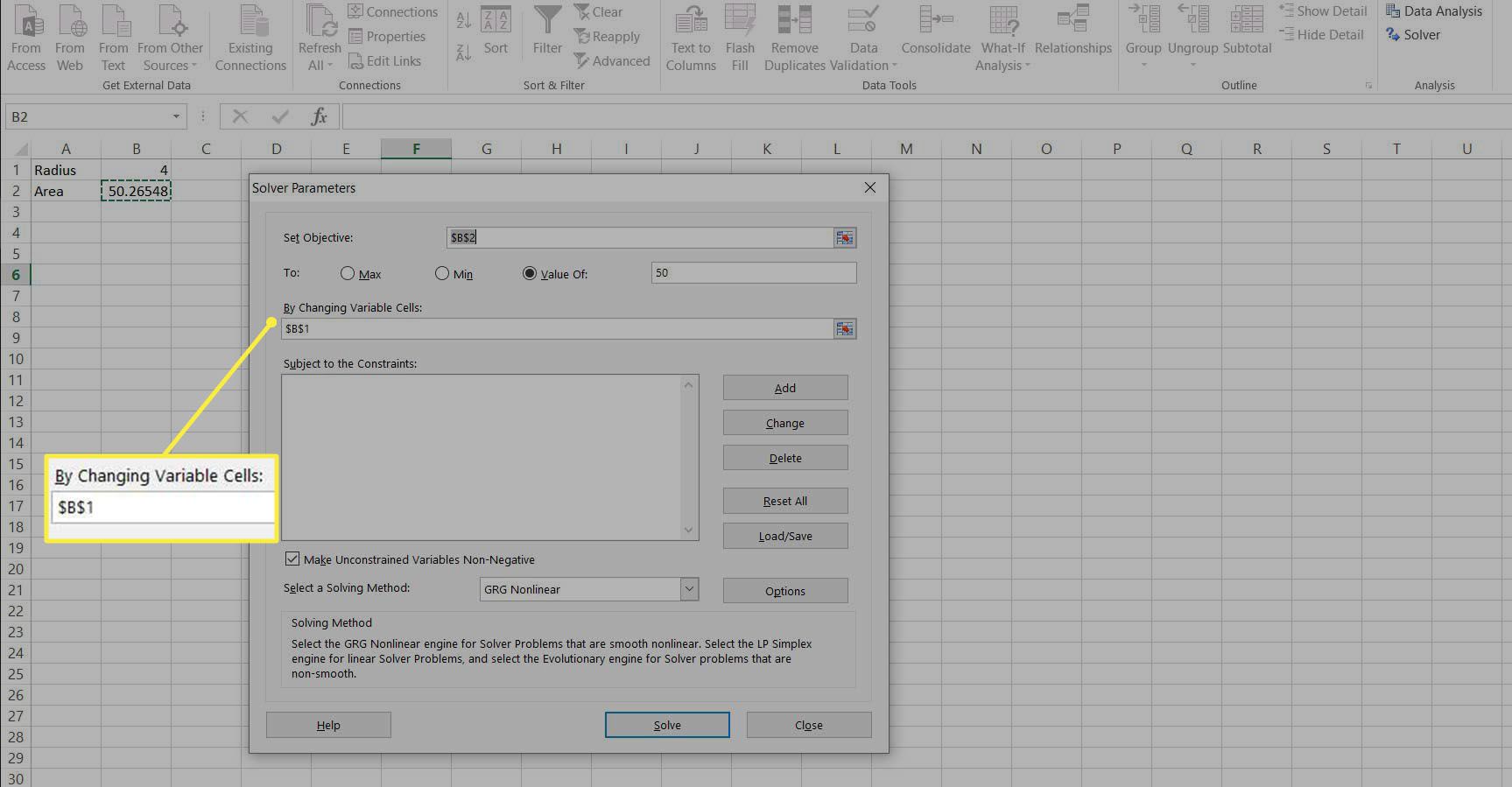
5. Jätä muut vaihtoehdot oletusarvoisesti ennalleen ja valitse Liuota† Optimointi suoritetaan, B1:n arvoa säädetään, kunnes B2 on 50 ja Ratkaisijoiden tulokset valintaikkuna tulee näkyviin.

   

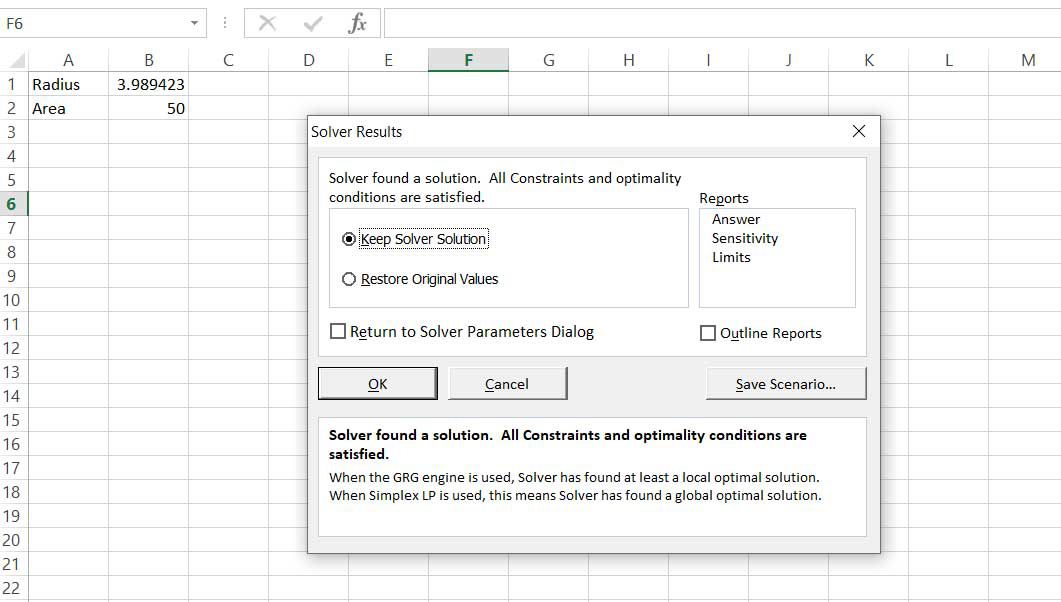
6. Valitse Okei ylläpitää ratkaisua.

   

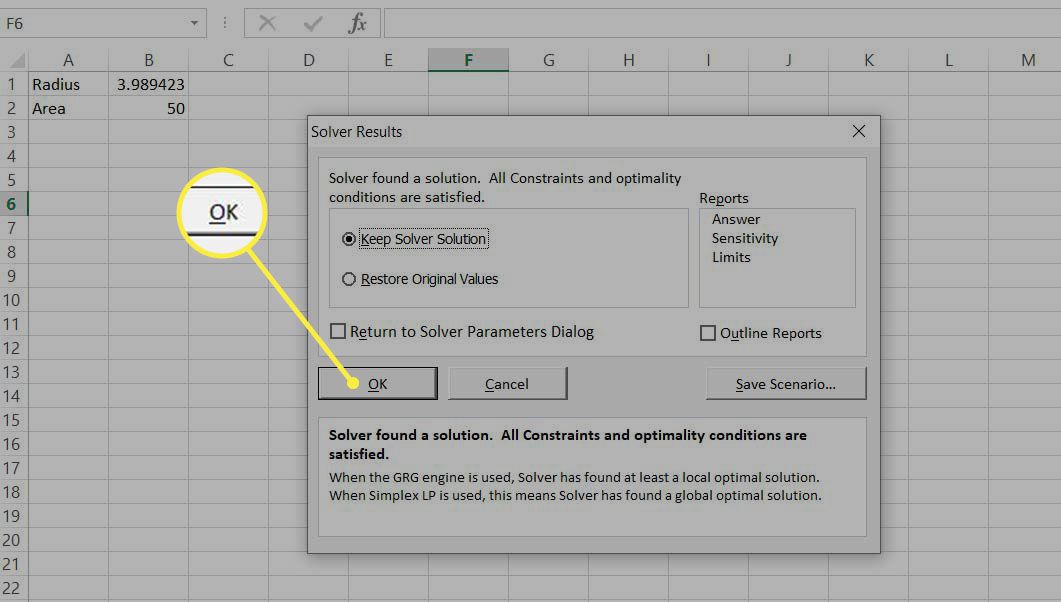
Tämä yksinkertainen esimerkki osoitti kuinka ratkaisija toimii. Tässä tapauksessa olisimme voineet saada ratkaisun helpommin muilla tavoilla. Seuraavaksi tarkastellaan joitain esimerkkejä, joissa Solver tarjoaa ratkaisuja, joita on muuten vaikea löytää.

Mukauta monimutkainen malli käyttämällä Excel Solver -apuohjelmaa

Excelissä on sisäänrakennettu ominaisuus lineaarisen regression suorittamiseen, joka säätää suoraa viivaa tietojoukon läpi. Monet yleiset epälineaariset funktiot voidaan linearisoida, mikä tarkoittaa, että lineaarista regressiota voidaan käyttää sovittamaan funktioita, kuten eksponentiaaleja. Monimutkaisempia toimintoja varten Ratkaisijaa voidaan käyttää «pienimmän neliösumman minimoimiseen». Tässä esimerkissä tarkastelemme muodon yhtälöä ax^b+cx^d alla olevista tiedoista.

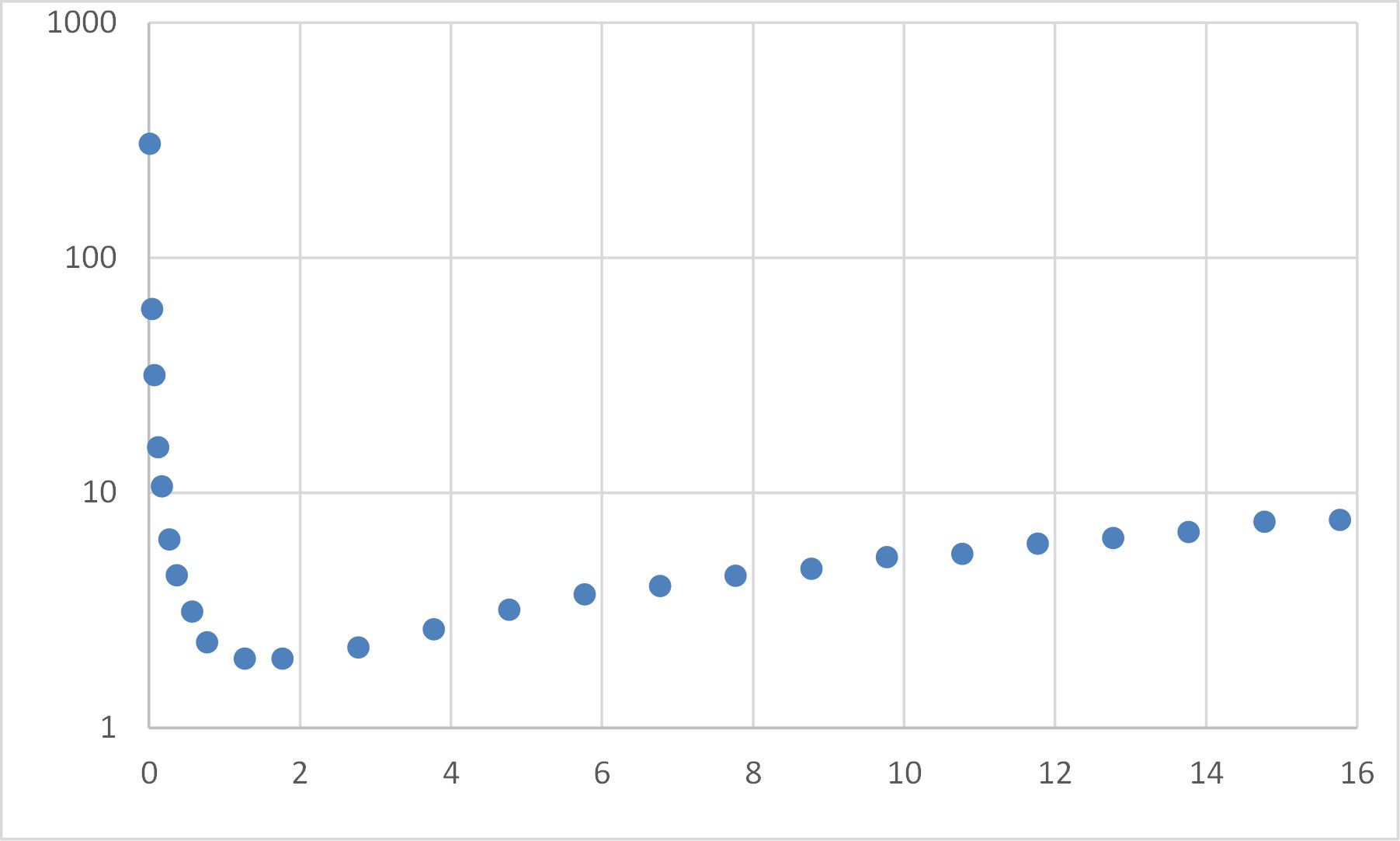
Se sisältää seuraavat vaiheet:

1. Järjestä tietojoukko sarakkeen A x-arvoilla ja sarakkeen B y-arvoilla.

2. Luo 4 kerroinarvoa (a, b, c ja d) jonnekin laskentataulukkoon, niille voidaan antaa mielivaltaisia ​​aloitusarvoja.

3. Luo mukautettujen Y-arvojen sarake käyttämällä yhtälöä muotoa ax^b+cx^d, joka viittaa vaiheessa 2 luotuihin kertoimiin ja sarakkeen A x-arvoihin. Huomaa, että syöttääksesi kaavan kopioi sarake, viittausten kertoimiin on oltava absoluuttisia, kun taas viittausten x-arvoihin on oltava suhteellisia.

   

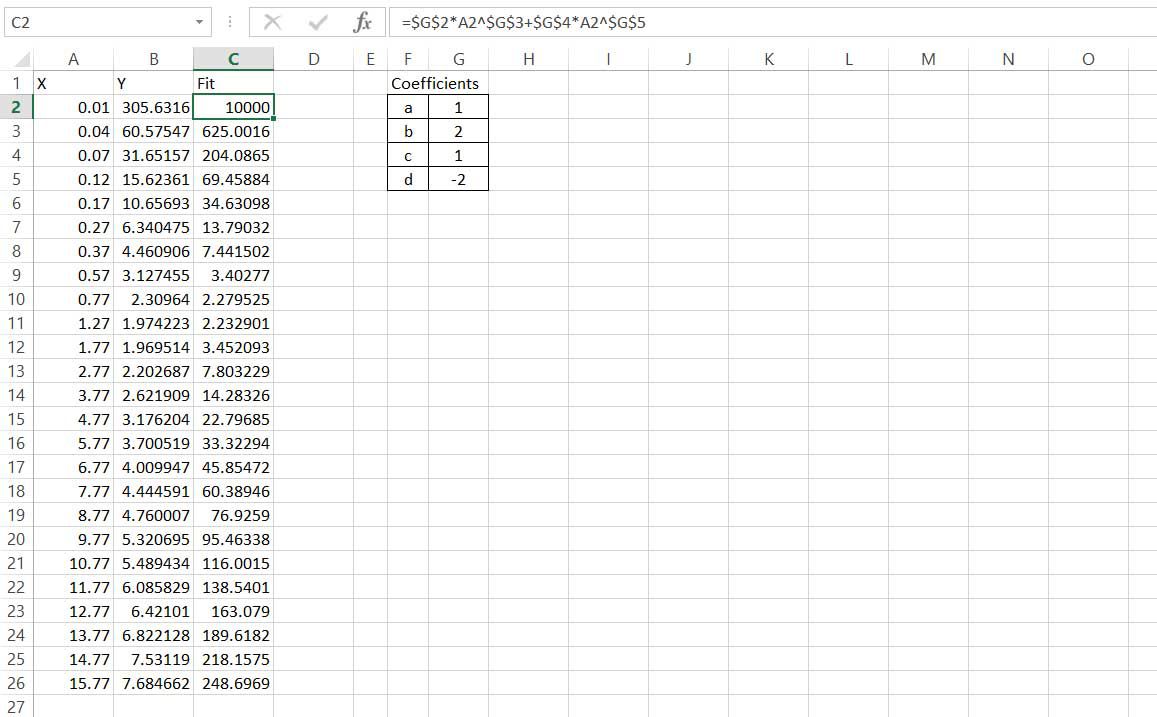
4. Vaikka se ei ole välttämätöntä, voit saada visuaalisen osoituksen yhtälön sopivuudesta piirtämällä molemmat y-sarakkeet x-arvoja vastaan ​​yhdellä XY-hajakuvaajalla. On järkevää käyttää merkkejä alkuperäisille datapisteille, koska ne ovat kohinaisia ​​diskreettejä arvoja, ja käyttää viivaa sopivaan vertailuun.

5. Seuraavaksi tarvitsemme tavan kvantifioida datan ja mukautetun yhtälömme välinen ero. Tavallinen tapa tehdä tämä on laskea neliöityjen erojen summa. Kolmannessa sarakkeessa kunkin rivin kohdalla Y:n alkuperäinen data-arvo vähennetään säädetystä vertailuarvosta ja tulos neliötetään. Joten sisään D2arvon antaa =(C2-B2)^2† Kaikkien näiden neliöllisten arvojen summa lasketaan sitten. Koska arvot ovat neliöity, ne voivat olla vain positiivisia.

   

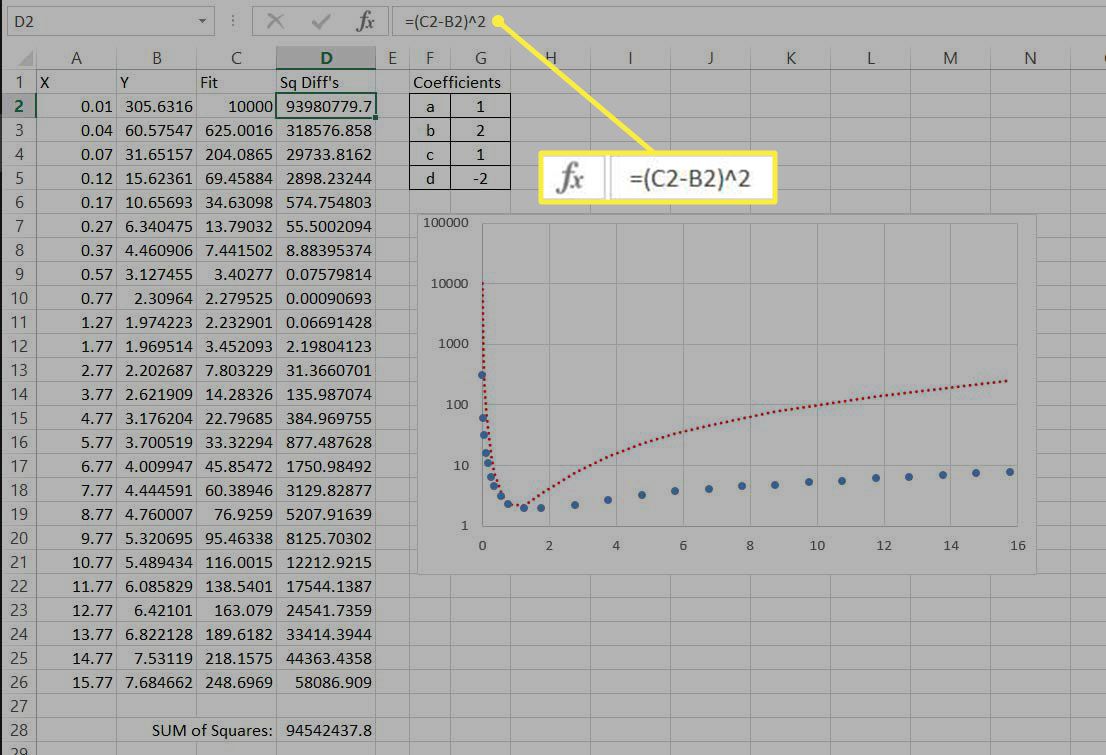
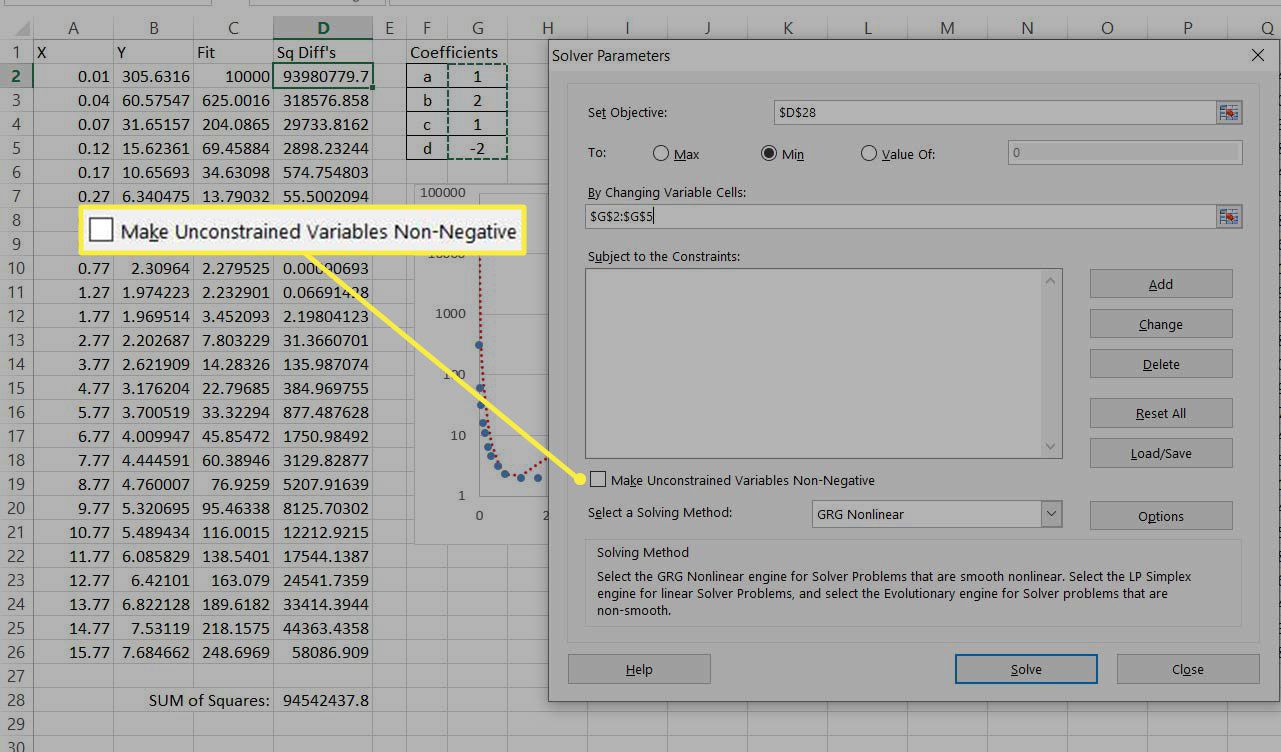
6. Olet nyt valmis suorittamaan optimoinnin Solverilla. On neljä kerrointa, joita on säädettävä (a, b, c ja d). Sinulla on myös yksi tavoitearvo minimoitavaksi, neliöityjen erojen summa. Käynnistä ratkaisija edellä kuvatulla tavalla ja aseta ratkaisijaparametrit viittaamaan näihin arvoihin alla olevan kuvan mukaisesti.

   

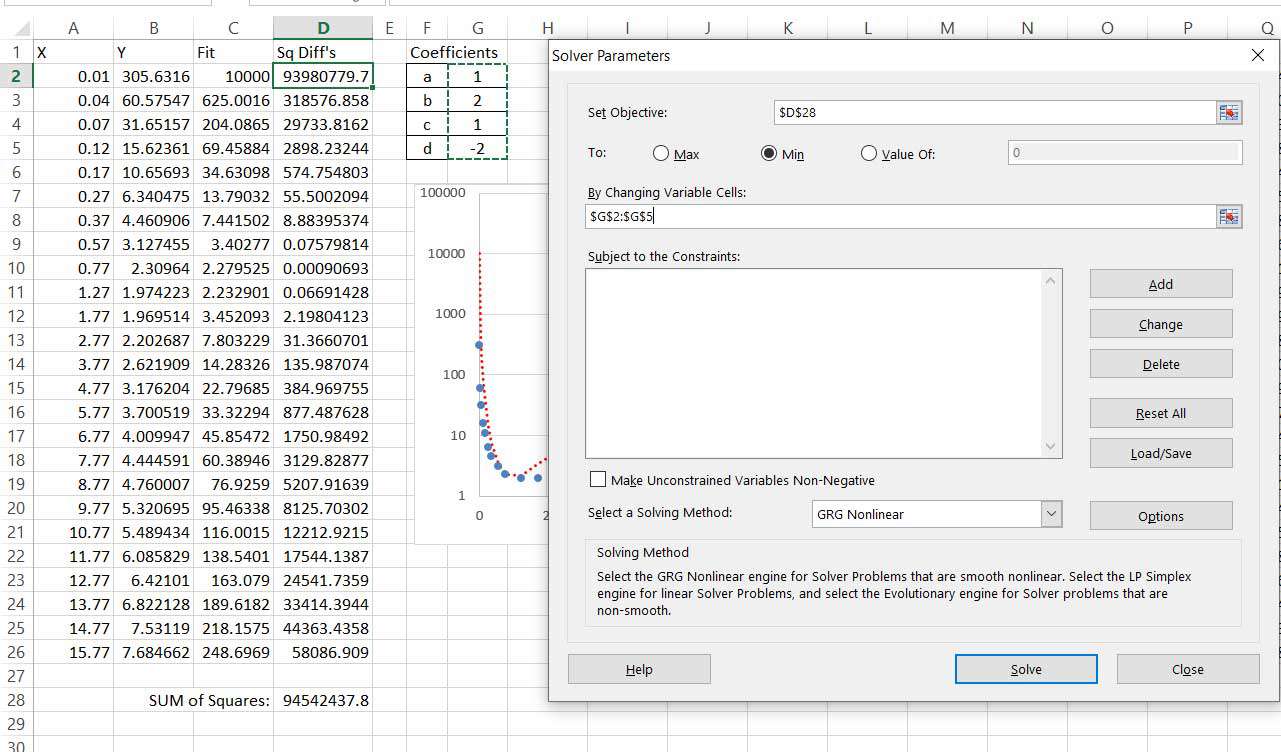
7. Poista vaihtoehto käytöstä Tee rajattomista muuttujista ei-negatiivisiatämä pakottaisi kaikki kertoimet ottamaan positiivisia arvoja.

   

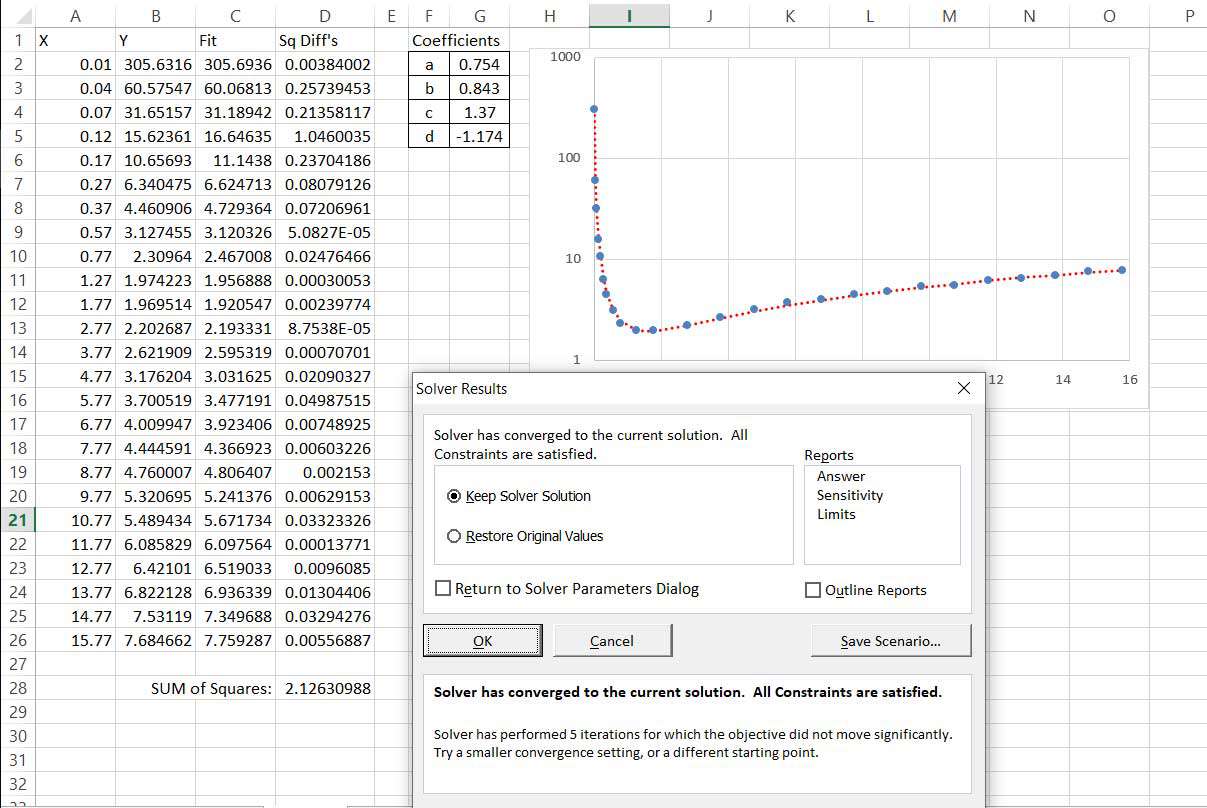
8. Valitse Liuota ja katso tulokset. Kaavio on päivitetty ja antaa hyvän kuvan hyvästä istuvuudesta. Jos ratkaisija ei sovi ensimmäisellä kerralla, voit yrittää suorittaa sen uudelleen. Jos istuvuus on parantunut, yritä ratkaista nykyisten arvojen perusteella. Muussa tapauksessa voit yrittää parantaa istuvuutta manuaalisesti ennen liuoksen liuottamista.

   

9. Kun hyvä istuvuus on saavutettu, voit poistua ratkaisijasta.

Ratkaise malli iteratiivisesti

Joskus on olemassa suhteellisen yksinkertainen yhtälö, joka antaa ulostulon syötteenä. Kuitenkin, kun yritämme kääntää ongelman, ei ole mahdollista löytää yksinkertaista ratkaisua. Esimerkiksi ajoneuvon likimääräinen tehonkulutus saadaan P = av + bv^3 missä v on nopeus, a on vierintävastuskerroin ja b on ilmanvastuskerroin. Vaikka tämä on melko yksinkertainen yhtälö, sitä ei ole helppo järjestää uudelleen antamaan yhtälö nopeudesta, jonka ajoneuvo saavuttaa tietyllä teholla. Voimme kuitenkin käyttää Ratkaisijaa löytääksemme tämän nopeuden iteratiivisesti. Etsi esimerkiksi nopeus, joka saavutetaan 740 W:n virrankulutuksella.

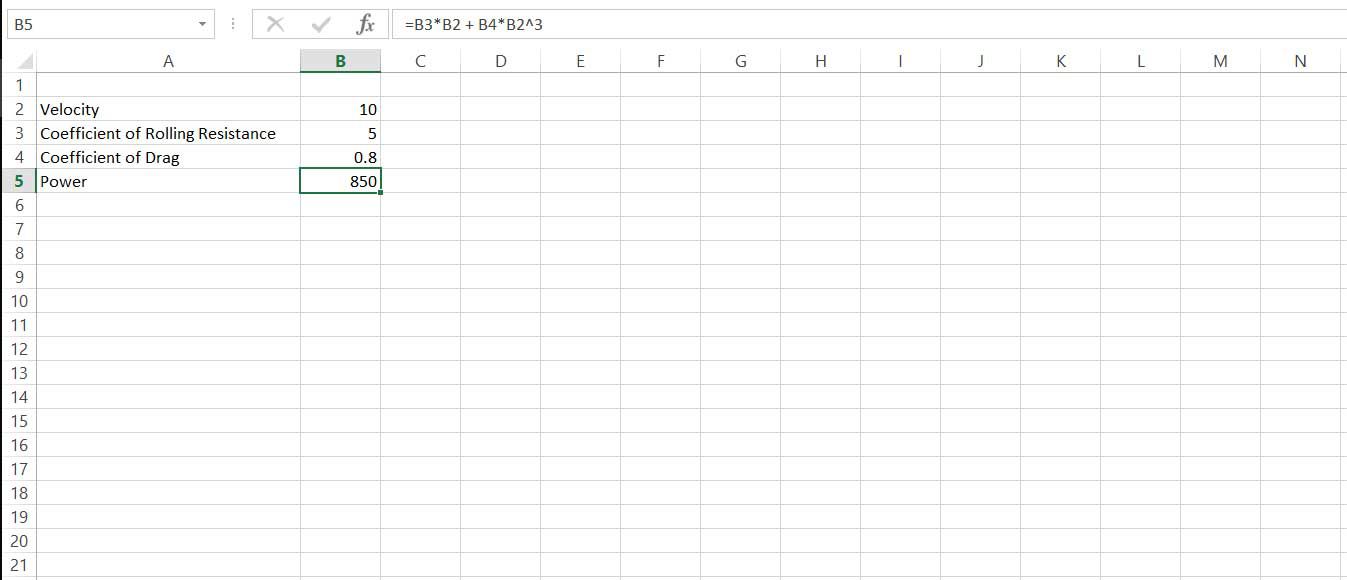
1. Tee yksinkertainen taulukko, jossa on nopeus, kertoimet a ja b sekä niistä laskettu teho.

   

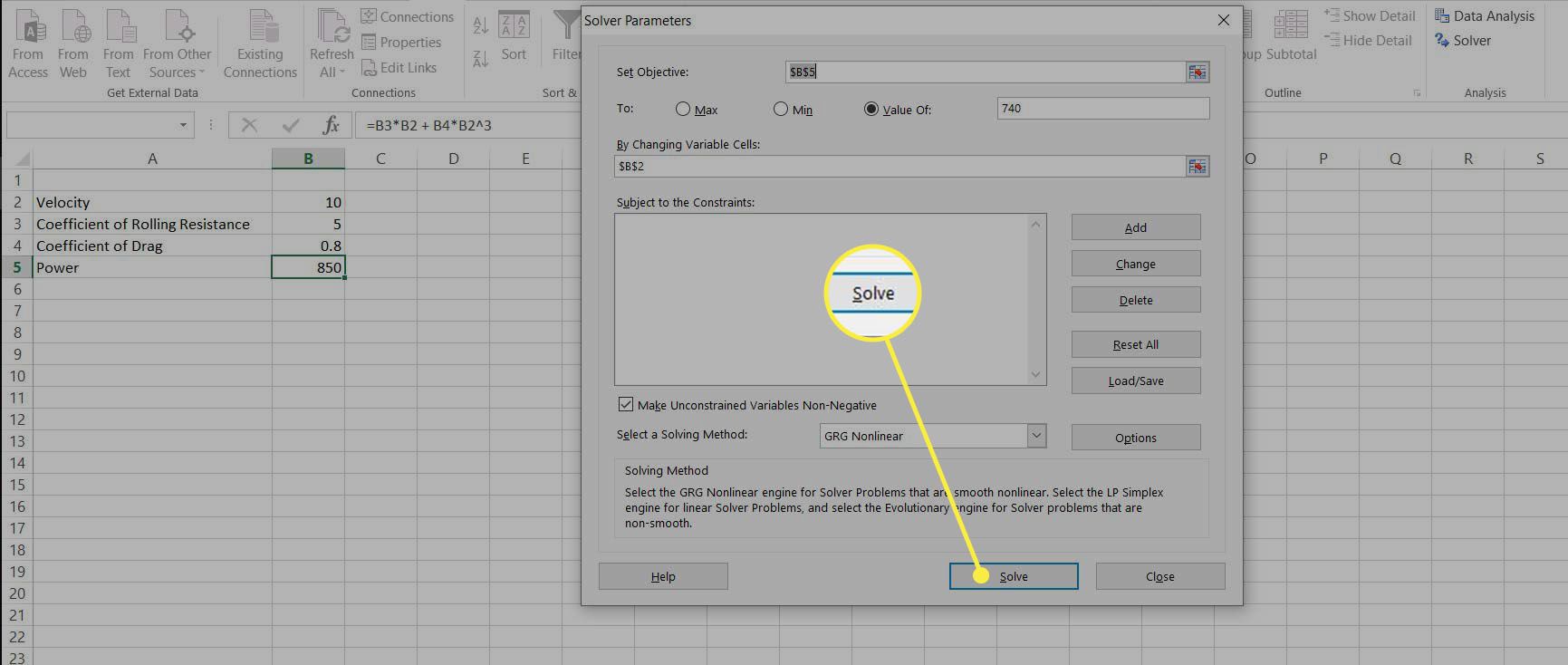
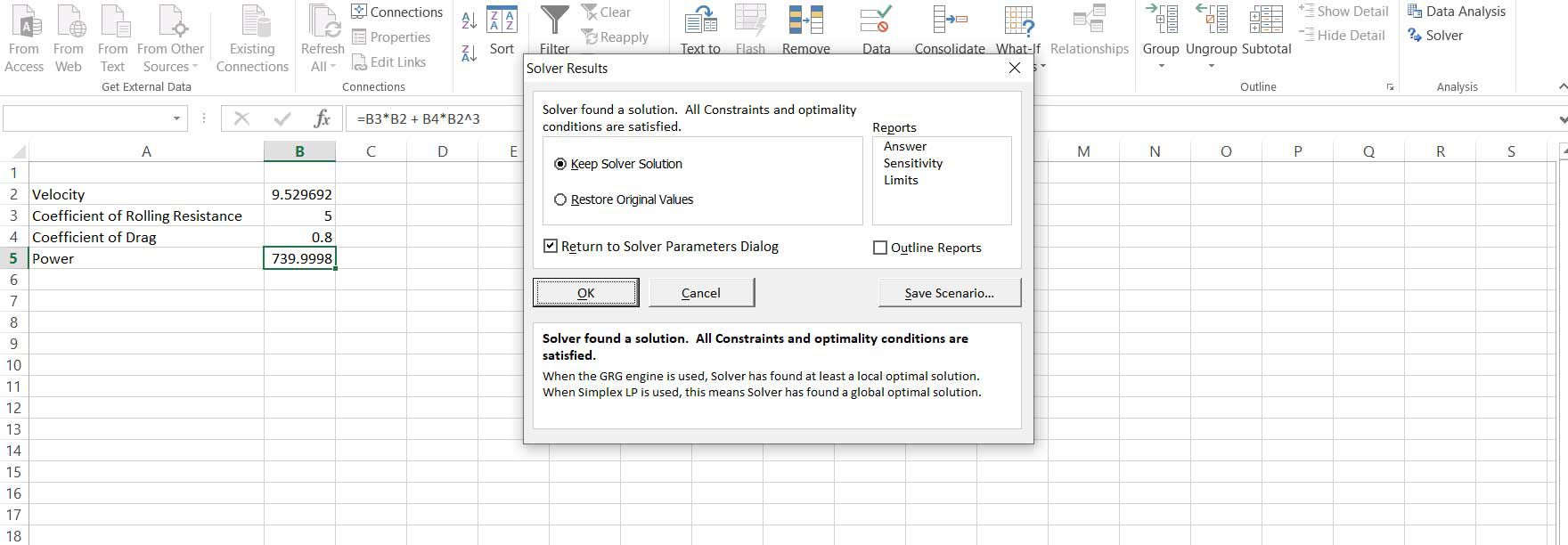
2. Käynnistä Ratkaisija ja syötä teho, B5, tavoitteena. Aseta objektiivinen arvo 740 ja valitse nopeus, B2, muuttuvina soluina. Valitse liueta aloittaa ratkaisun.

   

3. Ratkaisija säätää nopeuden arvoa, kunnes teho on hyvin lähellä arvoa 740, jotta voimme tarjota tarvitsemamme nopeuden.

   

4. Mallien ratkaiseminen tällä tavalla voi usein olla nopeampaa ja vähemmän virhealtista kuin monimutkaisten mallien kääntäminen.

Ratkaisijan eri vaihtoehtojen ymmärtäminen voi olla melko vaikeaa. Jos sinulla on vaikeuksia löytää järkevä ratkaisu, on usein hyödyllistä soveltaa rajaehtoja muuttuviin soluihin. Nämä ovat rajoja, joiden yli niitä ei saa muuttaa. Esimerkiksi edellisessä esimerkissä nopeus ei saisi olla pienempi kuin nolla ja olisi myös mahdollista asettaa yläraja. Tämä on nopeus, jota olet melko varma, että ajoneuvo ei voi ajaa sitä nopeammin. Jos pystyt asettamaan rajoituksia muuttuville muuttujasoluille, myös muut edistyneemmät vaihtoehdot, kuten multistart, toimivat. Tämä suorittaa useita erilaisia ​​ratkaisuja alkaen muuttujien erilaisista alkuarvoista. Myös ratkaisutavan valinta voi olla vaikeaa. Simplex LP sopii vain lineaarisille malleille, jos ongelma ei ole lineaarinen, se epäonnistuu ilmoittamalla, että tämä ehto ei täyty. Molemmat kaksi muuta menetelmää soveltuvat epälineaarisille menetelmille. GRG Nonlinear on nopein, mutta ratkaisu voi olla hyvin riippuvainen alkukäynnistysolosuhteista. Siinä on joustavuutta, koska se ei vaadi muuttujia rajojen asettamiseen. Evolutionary Solver on usein luotettavin, mutta se edellyttää, että kaikilla muuttujilla on sekä ylä- että alarajat, joita voi olla vaikea selvittää etukäteen. Excel Solver -apuohjelma on erittäin tehokas työkalu, jota voidaan soveltaa moniin käytännön ongelmiin. Kokeile yhdistää Ratkaisin Excel-makroihin, jotta voit käyttää Excelin tehoja täysimääräisesti.